본문 바로가기
알고리즘

최단 경로 찾기: 데이크스트라 알고리즘(Dijkstra Algorithm) 파이썬으로 구현하기

by ElectroPy 2019. 11. 5.

 

※해당 글은 네이버 블로그에서 작성된 글로, 가독성을 위해 아래 주소로 이동하여 보시는 것을 추천드립니다.

https://junwha0511.blog.me/221698256421

 

최단 경로 찾기: 데이크스트라 알고리즘(Dijkstra Algorithm) 파이썬으로 구현하기

안녕하세요! 최근 입시 때문에 많이 바빠서 블로그 포스팅을 못했습니다ㅠㅠㅠ​입시 준비를 하면서 다시 ...

blog.naver.com

안녕하세요! 최근 입시 때문에 많이 바빠서 블로그 포스팅을 못했습니다ㅠㅠㅠ

 

입시 준비를 하면서 다시 한번 살펴보았던 데이크스트라 알고리즘에 대해 포스팅하고자 합니다.

 

 

데이크스트라 알고리즘이란?

데이크스트라 알고리즘은 최단 경로를 찾는 알고리즘인데요,

 

그래프에 대한 선행 지식이 필요합니다.

https://junwha0511.blog.me/221698233962

 

 

 

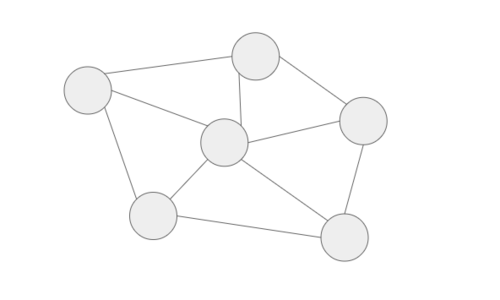
데이크스트라 알고리즘은 검색됨 플래그(Flag)를 기준으로 

최단 경로를 업데이트해나가는 방식입니다.

 

출처: 위키백과

 

데이크스트라 알고리즘의 과정

 

알고리즘의 처리 과정은 다음과 같습니다.

 

1. 시작점을 제외한 모든 정점의 Flag를 False로 놓습니다.

2. 시작점의 주변 정점들 중, 거리(가중치)가 최소인 정점을 다음 정점으로 잡습니다.

※ 다음 정점으로 선정된 정점은 Flag를 True로 놓고, 이전 정점의 최소 거리에 이전 정점부터 다음 정점까지의 거리(가중치)를 더한 값을 해당 정점의 최소 거리로 업데이트합니다.

3. Flag가 True인 정점들에서 갈 수 있는 정점들(Flag가 False인 정점이어야합니다.) 중, 거리가 최소인 정점을 다음 정점으로 선정합니다.

4. 다음 정점이 도착점일 경우 알고리즘을 종료하고, 도착점이 아닐 경우 3번을 반복합니다.

 

파이썬으로 구현하는 데이크스트라 알고리즘

 

데이크스트라 알고리즘은 다음 네가지 딕셔너리가 필요합니다.

 

1. 정점 간의 가중치를 저장할 딕셔너리

2. 정점의 Flag를 표시할 수 있는 딕셔너리

3. 정점까지의 최소 거리를 표시할 수 있는 딕셔너리

4. 최단 경로에 포함되는 정점들을 저장할 수 있는 딕셔너리

 

weight = {'A':{}, 'Z':{}} flag={'A':True, 'Z':False} dist={'A':0, 'Z':float('inf')} route=['Z']

 

 

네가지 딕셔너리를 위와 같이 선언한 후 그래프를 입력받습니다.

이 때 시작점은 A, 종착점은 Z로 고정합니다.

 

또한 각 최소 거리는 선정되기 전까지는 어떤 값보다도 커야하므로 무한값(float('inf'))으로 정의합니다.

 

print('input Graph(like A-B=1, but always A is start node and Z is destination)')
print('if you like to stop, input END')
while True:
	while True:
		line = input()
		if line == 'END':
			break
		else:
			node1 = line[line.index('-')-1]
			node2 = line[line.index('-')+1]
			weightValue = int(line[line.index('=')+1:])
			if not (node1 in weight):
				weight[node1] = {}
				flag[node1] = False
				dist[node1] = float('inf')
			if not (node2 in weight):
				weight[node2] = {}
				flag[node2] = False
				dist[node2] = float('inf')
			weight[node1][node2] = weightValue
			weight[node2][node1] = weightValue		
	print('Below is your graph, you like to stop? [Y/N]')
	print(weight)
	print(flag)
	print(dist)
	isYes = input()
	if isYes=='Y':
		break

 

 

Z의 Flag가 True가 될 때까지 반복되는 while문을 선언하고, 다음 정점 후보(nextNode)와 다음 최단거리 후보(nextDist)를 저장하는 변수를 선언합니다.

 

while not flag['Z']: 
	nextDist=float('inf') 
	nextNode=None

 

 

전체 정점(Flag의 모든 Key값) 중 Flag가 True인 지점과 연결된 정점들(Weight 딕셔너리에 Key를 넣었을 때 나오는 하위 Key들) 중, Flag가 False인 정점들에 대해 For문을 수행합니다.

 

For문 내부에서는 cDist(비교할 거리)를 (이전 최소 거리+이전 정점부터 다음 정점까지의 가중치)로 정의하고,

 

cDist가 앞에서 정의했던 '다음 최단 거리 후보'보다 작으면 다음 최단 거리 후보를 cDist로 업데이트하고, 다음 정점 후보를 해당 정점으로 업데이트합니다.

 

	for key in flag.keys():
		if flag[key]:
			for node in weight[key]:
				if not flag[node]:
					cDist=dist[key]+weight[key][node]
					if cDist<nextDist:
						nextNode=node
						nextDist=cDist

 

 

for문이 모두 끝나면 다음 정점 후보(nextNode)와 다음 최단 거리 후보(nextDist)에 최단 경로가 저장이 됩니다.

따라서 노드와 최단 경로를 업데이트해줍니다.

	dist[nextNode]=nextDist
	flag[nextNode]=True

 

 

이러한 과정을 거쳐 while문이 Z 정점에 도달하게 되면 dist 딕셔너리에는 각 정점까지의 최단 경로가, flag에는 활성화 된 정점들이 True 상태로 있게 됩니다.

데이크스트라 알고리즘은 최단 '경로'를 찾는 알고리즘이므로 앞서 얻은 정보로 최단 경로를 출력하여야 합니다.

 

최단 경로를 찾는 방법은 Back-Tracking을 사용합니다.

출발점에서는 선택지가 여러개이지만, 도착점에서는 선택지가 한개라는 아이디어를 이용한 방법입니다.

현재 정점의 최단 거리에서 이전 정점까지의 가중치를 뺀 값이 이전 정점의 최단 거리와 일치하면

해당 정점을 route 리스트의 첫번째에 추가하고 Flag를 False로 전환합니다.

정점 A가 False가 되면 route 배열에는 최단 경로가 저장되게 됩니다.

최단 거리는 dist['Z']입니다.

 

while flag['A']:
	for node in weight[ptd]:
		if (dist[ptd]-weight[ptd][node])==dist[node]:
			route.insert(0,node)
			flag[node]=False
			ptd=node
			break	
print(dist['Z'])
print(route)

 

코드 전문

weight = {'A':{}, 'Z':{}}
flag={'A':True, 'Z':False}
dist={'A':0, 'Z':float('inf')}
route=['Z']
ptd='Z'

print('input Graph(like A-B=1, but always A is start node and Z is destination)')
print('if you like to stop, input END')
while True:
	while True:
		line = input()
		if line == 'END':
			break
		else:
			node1 = line[line.index('-')-1]
			node2 = line[line.index('-')+1]
			weightValue = int(line[line.index('=')+1:])
			if not (node1 in weight):
				weight[node1] = {}
				flag[node1] = False
				dist[node1] = float('inf')
			if not (node2 in weight):
				weight[node2] = {}
				flag[node2] = False
				dist[node2] = float('inf')
			weight[node1][node2] = weightValue
			weight[node2][node1] = weightValue		
	print('Below is your graph, you like to stop? [Y/N]')
	print(weight)
	print(flag)
	print(dist)
	isYes = input()
	if isYes=='Y':
		break

while not flag['Z']:
	nextDist=float('inf')
	nextNode=None
	for key in flag.keys():
		if flag[key]:
			for node in weight[key]:
				if not flag[node]:
					cDist=dist[key]+weight[key][node]
					if cDist<nextDist:
						nextNode=node
						nextDist=cDist
	dist[nextNode]=nextDist
	flag[nextNode]=True


while flag['A']:
	for node in weight[ptd]:
		if (dist[ptd]-weight[ptd][node])==dist[node]:
			route.insert(0,node)
			flag[node]=False
			ptd=node
			break	
print(dist['Z'])
print(route)

이상으로 포스팅을 마치도록 하겠습니다.

이해가 안되는 부분이 있다면 댓글로 질문 부탁드립니다:)

 

댓글

티스토리툴바